An introduction to Multi-Armed Bandits for Wireless Communications
Francesc Wilhelmi

Full presentation available here
PART I
Bandits Theory
- The Multi-Armed Bandits (MABs) problem addresses the exploration-exploitation trade-off in face of uncertainty
- Classically, a gambler attempts to maximize the profits among a set of slot machines
- Often, we refer to the expected cumulative regret to quantify the performance of a given action-selection strategy
- Take the oracle’s policy as a reference
- Convergence analysis: anytime, fixed-horizon or asymptotic optimality
- MABs are a class of sequential learning framework that allow to address the tradeoff between exploration and exploitation in face of uncertainty
- Suits problems with unavailable or incomplete information
- There’s no need of modeling states or trying to learn them (which entails added complexity)
- Many different MABs-based models have been provided for several types of problems
- Baseline:
- Katehakis, M. N., & Veinott Jr, A. F. (1987). The multi-armed bandit problem: decomposition and computation. Mathematics of Operations Research, 12(2), 262-268.
- Gittins, J., Glazebrook, K., & Weber, R. (2011). Multi-armed bandit allocation indices. John Wiley & Sons.
- Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multiarmed bandit problem. Machine learning, 47(2-3), 235-256.
- Auer, P., Cesa-Bianchi, N., Freund, Y., & Schapire, R. E. (1995, October). Gambling in a rigged casino: The adversarial multi-armed bandit problem. In Foundations of Computer Science, 1995. Proceedings., 36th Annual Symposium on (pp. 322-331). IEEE.
- Overviews:
- Bubeck, S., & Cesa-Bianchi, N. (2012). Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Foundations and Trends® in Machine Learning, 5(1), 1-122.
- Vermorel, J., & Mohri, M. (2005, October). Multi-armed bandit algorithms and empirical evaluation. In European conference on machine learning (pp. 437-448). Springer, Berlin, Heidelberg.
MABs Taxonomy
- Stochastic
- The reward is generated according to a specific stochastic process
- Literature: [5]
- Non-stochastic:
- No statistic assumption can be done on the reward generation process
- Literature: [5, 7]
- More subtle categorization on reward generating process:
- Stateful (Markovian): every arm is associated with some finite state space
- Stateless: arms do not have specific state
- Adversarial: different learners attempt to maximize a given reward function
- Other types:
- Contextual: in addition to the reward, some other useful information is provided to the agent
- Combinatorial: there is a relationship between arms
- Mortal: arms are available for a certain amount of time
- ...
- Stateful (Markovian)
- Rested (frozen/sleeping): the state of a given arm only changes when pulled
- Restless: the state of every arm changes regardless of the player’s action
- Stateless (Stochastic)
- The reward generation process is stochastic (stationary or non-stationary density function), and is independent and identically distributed (IID)
- Adversarial
- Rewards generation cannot be attributed to any stochastic assumption: Oblivious adversaries / Non-oblivious adversaries (min-max strategies)
- Contextual bandits [8-9]:in addition to the reward, some other useful information is provided to the agent
- Combinatorial bandits [10-11]: there is a relationship between arms
- Mortal bandits [12]: arms are available for a certain amount of time
- MABs with multiple plays [13-15]: a player can pick several arms simultaneously
- Pure exploration [16-17]: gain the most knowledge over t by exploring, in order to maximize the likelihood of picking the best arm in t+1
- Dueling bandits [18]: the player chooses a pair of arms in each round and observe only their performances (duel between arms)
Well-known Algorithms
Greedy learning
- ε-greedy [29]
- With probability ε, choose xt ~ Unif(X),
- Otherwise, choose xt ∈ argmaxx f̂t
- Explores inefficiently
- With fixed ε, the average regret grows linearly
- Time-dependent exploration rate favors efficiency: εt = ε0/t
Optimistic learning
- Upper Confidence Bound (UCB) [3, 28]
- Assumes certain distributions for the rewards and picks the optimal arm accordingly
- The action-selection process not only takes the magnitude of the reward into account, but the estimated deviations
Probability Matching learning
- Thompson sampling [30]
- Has been shown to achieve strong performance guarantees, often better than those warranted by UCB [31, 32, 33]
- It constructs a probabilistic model of the rewards and assumes a prior distribution of the parameters of said model – Then, it chooses the arm matching the probability of being optimal
- Very popular because it is computationally cheap and offers good results
Single-Agent vs Multi-Agent MABs
- SA-MAB: mainly concerned on sequential online decision making problem in an unknown environment
- MA-MAB: where Game Theory and MABs meet and complement each other (competition between agents)
Single-Agent
- Baseline: [19, 20]
- Properties:
- Stationarity of the environment
- Pure exploration-exploitation
- The Regret measurement is completely meaningful in this setting
- State-of-the-Art performance bounds:
- Lai and Robbins, 1985
- Anantharam et al., 1987 (multiple plays)
Multi-Agent
- Properties:
- Non-stationarity of the environment
- Nexus with Game Theory
- Adversarial MABs is a sub-class of the Multi-Agent MAB problem
- Models:
- Decentralized – Selfish behavior
- Distributed – Communication among agents
- Centralized – Correlated Equilibria
Adversarial MABs
- Adversarial MABs typically frame to decentralized/distributed problems, where different learners compete for the same resources
- According to the way rewards are revealed, we find:
- Full information game: the player knows the reward of all the actions
- Partial information game: the player only knows the reward of the played action
- The notions of Internal and External regret are very important
Nexus with Game Theory
- N-player game whereby player i competes with N-1 opponents
- The goal is to determine convergence to some kind of equilibrium
- In two-person zero-sum games, NE can be achieved if both players adopt an external-regret minimizing strategy. However, this does not hold for general N-player games!
- We need to provide internal-regret minimizing strategies in order to converge to a Correlated Equilibrium (holds for the empirical joint frequencies)
Internal and External regret
| Internal Regret | External Regret |
|---|---|
| Compares the loss incurred by changing actions in a pairwise manner | Compares the expected reward of the actual mixed strategy with the best action |
External-regret minimizing Algorithms
- Weighted Average Prediction (WAP)
- Hedge [4], variant of [21] for full information games
- EXP3 [2]
- Following the Perturbed Leader (FPL) [22], an online learning extension of [23]
- Implicitly Normalized Forecaster (INF) Algorithm [24, 25]
- Internal-Regret Minimizing Algorithm [26]
Internal-regret minimizing Algorithms
- External-regret minimizing algorithms have been shown to work only for N = 2 players, thus NE or CE cannot be guaranteed for N ≥ 3
- However, if every player uses an internal-regret minimizing strategy, “the joint empirical frequencies of plays converge to a correlated equilibrium”
- The Experimental Regret Testing (ERT) [27] has been shown to exhibit internal-regret minimization
PART II
Bandits in Wireless Communications
Previous Work
- MP-MABs for Opportunistic Spectrum Access [34-38]
- Joint Channel Selection and Power Control in Cognitive Radio Networks [39]
- Distributed inter-cell interference coordination [40]
- Distributed user association in small cell networks [41]
- Multi-path routing [42]
- Dynamic rate and channel selection [43]
- Unlicensed LTE/WiFi Coexistence [44]
- Cognitive Radio problems have raised attention, due to its decentralized (or distributed) nature
- Therefore, the MP-MABs setting have been shown to properly fit to Cognitive Radio Networks
- Several efforts have been done to provide mechanisms whereby multiple users converge to the optimal solution
- Baseline [45]
- Combinatorial approach [46, 47]
- TDFS approach [48]
- User-specific penalties [39]
- Calibrated Forecasting [37]
Previous considerations
Remarkable guarantees (convergence, performance, etc.) are often achieved only if certain assumptions hold:
| Assumption | Drawbacks |
|---|---|
| All the players use the same strategy | Not feasible in dense and heterogeneous scenarios |
| The number of users is fixed and known | While the former implies that the network remains static, the latter entails communication or additional hardware |
| User-specific penalties are applied | A strong knowledge on the scenario must be known on before-hand |
| The reward generation process is relaxed and only depends on the own actions | Unfeasible in potentially overlapping scenarios, where the outer interference severely affects to the performance of a given WN |
Reward Distributions
- Typical action-selection strategies assume well-known distributions (e.g., Gaussian) for the reward, which allows to effectively address the exploration-exploitation trade-off
- However, reward distributions are hard to model in WNs, especially in adversarial environments
- Then, performance guarantees cannot be assured
- Nevertheless, good results have been shown on assuming Gaussian distributions for the Spatial Reuse problem [49, 50]
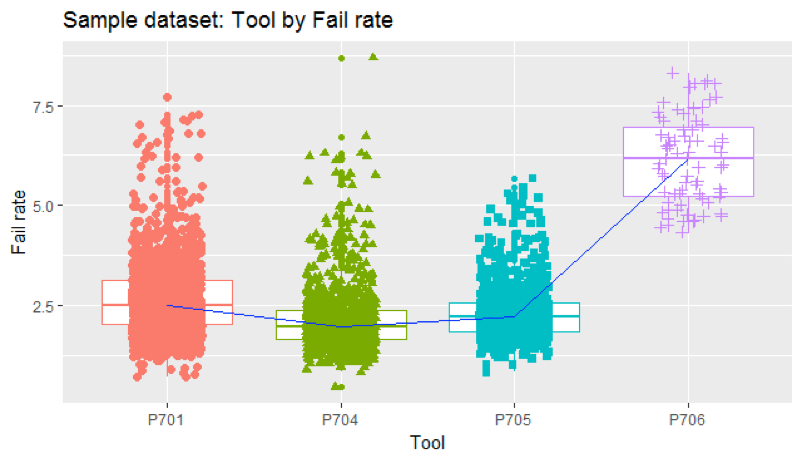
Use Case
Learning in Adversarial WLANs
- In practice, the AP may incorporate an agent that performs learning operations according to the information received
- Extensions of the decentralized case would entail communication and cooperation between agents
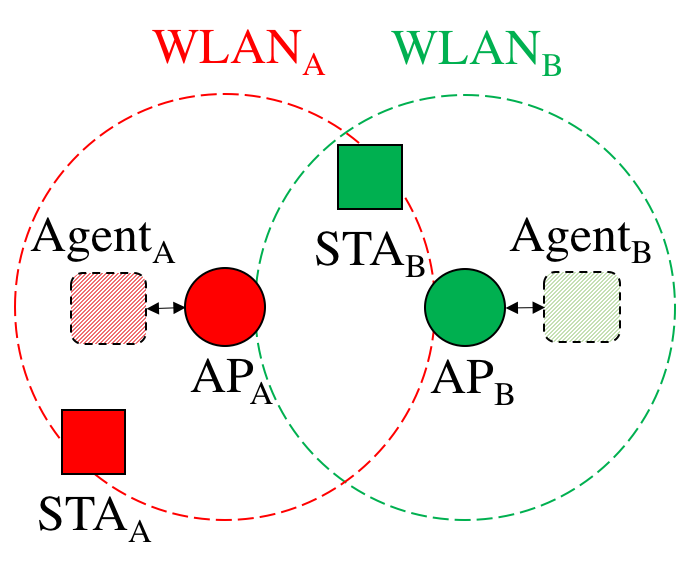
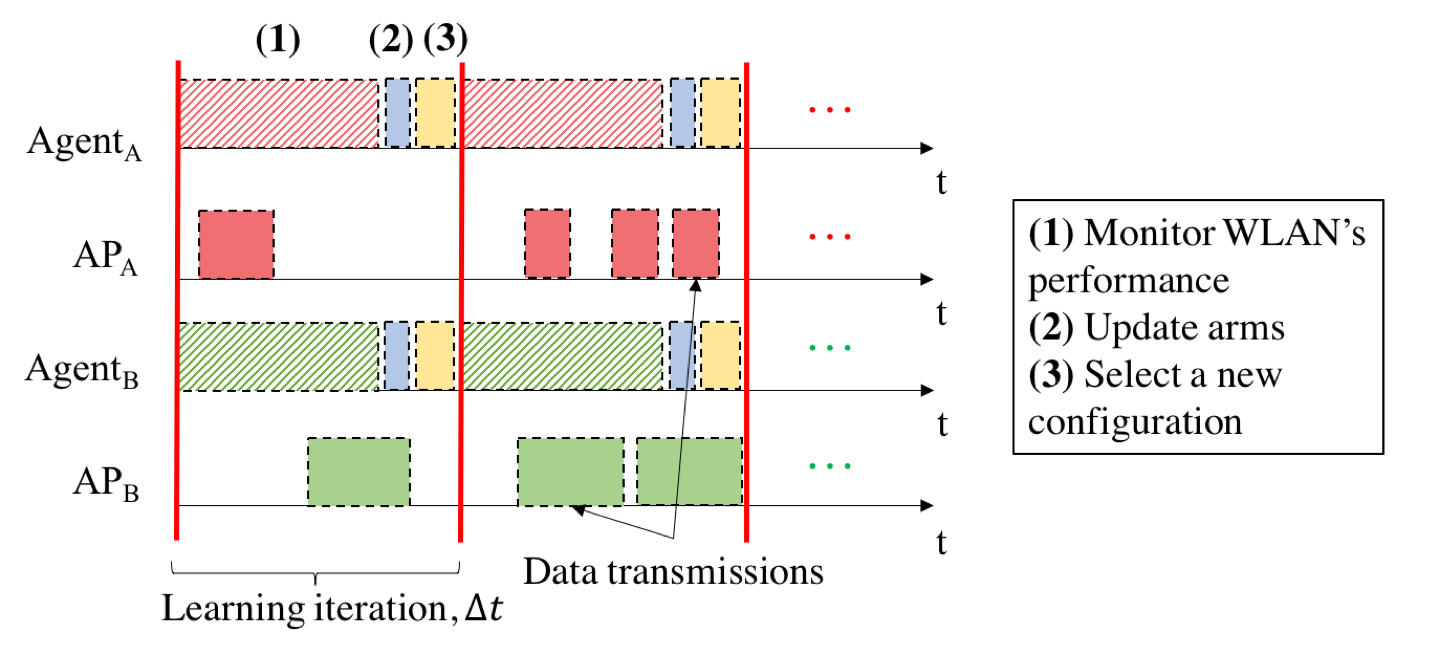
MABs formulation
- Let there be 𝒩={1, …, 𝑁} the set of potentially overlapping WLANs
- Each WLAN can choose from a range of actions 𝒜={1, …, 𝐾}, which refer to certain configurations (e.g., transmit power)
- Initially, the estimate reward of each action available in any WLAN, k∈{1, …, 𝐾}, is set to 0
- At every iteration, each WLAN selects an arm randomly according its action selection-strategy
- After choosing an action k at iteration t, each WLAN observes the reward generated by the environment, rk,t, which is based on the experienced throughput that depends on 1) its own action and 2) the actions made by the overlapping WLANs
- The new information is used for updating the knowledge on the available arms
Reward Generation
- The reward is generated after a WLAN (or a set of WLANs) makes an action
- It may be “selfish” or “collaborative”, according to the performance measure considered
- The reward quantifies the performance experienced by the WLAN, so it may refer to:
- Throughput
- Packets sent
- Delay
- ...
Reward Normalization
- It is very important to normalize the obtained reward (which may be of great magnitude), in order to let the algorithms operate properly
- However, normalization is done according to the optimal performance, which may be unknown and unfeasible to be derived
- Thus, reasonable upper bounds can be provided for normalization
- Maximum achievable data rate
- Theoretical capacity
- ...
Some Conclusions
- The learning process in wireless networks can be really slow
- We need to question ourselves: is it worth?
- Convergence guarantees may not exist, neither logarithmic regret decreasing
- Decentralized settings are, in practice, unfeasible
- However, performance maximization can be provided
- Feasibility of applying learning in wireless networks
- Distributed (message exchanging)
- Centralized system (correlated equilibrium)
References
[1] Katehakis, M. N., & Veinott Jr, A. F. (1987). The multi-armed bandit problem: decomposition and computation. Mathematics of Operations Research, 12(2), 262-268.
[2] Gittins, J., Glazebrook, K., & Weber, R. (2011). Multi-armed bandit allocation indices. John Wiley & Sons.
[3] Auer, P., Cesa-Bianchi, N., & Fischer, P. (2002). Finite-time analysis of the multiarmed bandit problem. Machine learning, 47(2-3), 235-256.
[4] Auer, P., Cesa-Bianchi, N., Freund, Y., & Schapire, R. E. (1995, October). Gambling in a rigged casino: The adversarial multi-armed bandit problem. In Foundations of Computer Science, 1995. Proceedings., 36th Annual Symposium on (pp. 322-331). IEEE.
[5] Bubeck, S., & Cesa-Bianchi, N. (2012). Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Foundations and Trends® in Machine Learning, 5(1), 1-122.
[6] Vermorel, J., & Mohri, M. (2005, October). Multi-armed bandit algorithms and empirical evaluation. In European conference on machine learning (pp. 437-448). Springer, Berlin, Heidelberg.
[7] Auer, Peter, et al. "The nonstochastic multiarmed bandit problem." SIAM journal on computing 32.1 (2002): 48-77.
[8] Slivkins, A. (2014). Contextual bandits with similarity information. Journal of Machine Learning Research, 15(1), 2533-2568.
[9] Agrawal, S., & Goyal, N. (2013, February). Thompson sampling for contextual bandits with linear payoffs. In International Conference on Machine Learning (pp. 127-135).
[10] Cesa-Bianchi, N., & Lugosi, G. (2012). Combinatorial bandits. Journal of Computer and System Sciences, 78(5), 1404-1422.
[11] Chen, W., Wang, Y., & Yuan, Y. (2013, February). Combinatorial multi-armed bandit: General framework and applications. In International Conference on Machine Learning (pp. 151-159).
[12] Chakrabarti, D., Kumar, R., Radlinski, F., & Upfal, E. (2009). Mortal multi-armed bandits. In Advances in neural information processing systems (pp. 273-280).
[13] Anantharam, V., Varaiya, P., & Walrand, J. (1987). Asymptotically efficient allocation rules for the multiarmed bandit problem with multiple plays-Part I: IID rewards. IEEE Transactions on Automatic Control, 32(11), 968-976.
[14] Anantharam, V., Varaiya, P., & Walrand, J. (1987). Asymptotically efficient allocation rules for the multiarmed bandit problem with multiple plays-Part II: Markovian rewards. IEEE Transactions on Automatic Control, 32(11), 977-982.
[15] Komiyama, J., Honda, J., & Nakagawa, H. (2015). Optimal regret analysis of thompson sampling in stochastic multi-armed bandit problem with multiple plays. arXiv preprint arXiv:1506.00779.
[16] Bubeck, S., Munos, R., & Stoltz, G. (2011). Pure exploration in finitely-armed and continuous-armed bandits. Theoretical Computer Science, 412(19), 1832-1852.
[17] Chen, S., Lin, T., King, I., Lyu, M. R., & Chen, W. (2014). Combinatorial pure exploration of multi-armed bandits. In Advances in Neural Information Processing Systems (pp. 379-387).
[18] Yue, Y., Broder, J., Kleinberg, R., & Joachims, T. (2012). The k-armed dueling bandits problem. Journal of Computer and System Sciences, 78(5), 1538-1556.
[19] Robbins, H. (1985). Some aspects of the sequential design of experiments. In Herbert Robbins Selected Papers (pp. 169-177). Springer, New York, NY.
[20] Thompson, W. R. (1933). On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3/4), 285-294.
[21] Littlestone, N., & Warmuth, M. K. (1994). The weighted majority algorithm. Information and computation, 108(2), 212-261.
[22] Kujala, J., & Elomaa, T. (2007, October). Following the perturbed leader to gamble at multi-armed bandits. In International Conference on Algorithmic Learning Theory (pp. 166-180). Springer, Berlin, Heidelberg.
[23] Hannan, J. (1957). Approximation to Bayes risk in repeated play. Contributions to the Theory of Games, 3, 97-139.
[24] Audibert, J. Y., & Bubeck, S. (2009, June). Minimax policies for adversarial and stochastic bandits. In COLT (pp. 217-226).
[25] Audibert, J. Y., & Bubeck, S. (2010). Regret bounds and minimax policies under partial monitoring. Journal of Machine Learning Research, 11(Oct), 2785-2836.
[26] Stoltz, G., & Lugosi, G. (2005). Internal regret in on-line portfolio selection. Machine Learning, 59(1-2), 125-159.
[27] Cesa-Bianchi, N., & Lugosi, G. (2006). Prediction, learning, and games. Cambridge university press.
[28] Agrawal, R. (1995). Sample mean based index policies by o (log n) regret for the multi-armed bandit problem. Advances in Applied Probability, 27(4), 1054-1078.
[29] Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction (Vol. 1, No. 1). Cambridge: MIT press.
[30] William R Thompson. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3/4):285–294, 1933.
[31] Shipra Agrawal and Navin Goyal. Analysis of thompson sampling for the multi-armed bandit problem. In Conference on Learning Theory, pages 39–1, 2012.
[32] Emilie Kaufmann, Nathaniel Korda, and R´emi Munos. Thompson sampling: An asymptotically optimal finite time analysis. In Algorithmic Learning Theory, pages 199–213. Springer, 2012.
[33] Nathaniel Korda, Emilie Kaufmann, and Remi Munos. Thompson sampling for 1- dimensional exponential family bandits. In C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q. Weinberger, editors, Advances in Neural Information Processing Systems 26, pages 1448–1456. Curran Associates, Inc., 2013.
[34] Keqin Liu and Qing Zhao. Distributed learning in multi-armed bandit with multiple players. IEEE Transactions on Signal Processing, 58(11):5667–5681, 2010.
[35] Animashree Anandkumar, Nithin Michael, Ao Kevin Tang, and Ananthram Swami. Distributed algorithms for learning and cognitive medium access with logarithmic regret. IEEE Journal on Selected Areas in Communications, 29(4):731–745, 2011.
[36] Jonathan Rosenski, Ohad Shamir, and Liran Szlak. Multi-player bandits–a musical chairs approach. In International Conference on Machine Learning, pages 155–163, 2016.
[37] Setareh Maghsudi and Slawomir Stanczak. Channel selection for network-assisted D2D communication via no-regret bandit learning with calibrated forecasting. IEEE Transactions on Wireless Communications, 14(3):1309–1322, 2015.
[38] Di Felice, M., Chowdhury, K. R., & Bononi, L. (2011, December). Learning with the bandit: A cooperative spectrum selection scheme for cognitive radio networks. In Global Telecommunications Conference (GLOBECOM 2011), 2011 IEEE (pp. 1-6). IEEE.
[39] Setareh Maghsudi and Slawomir Stanczak. Joint channel selection and power control in infrastructureless wireless networks: A multiplayer multiarmed bandit framework. IEEE Transactions on Vehicular Technology, 64(10):4565–4578, 2015.
[40] Coucheney, P., Khawam, K., & Cohen, J. (2015, June). Multi-Armed Bandit for distributed Inter-Cell Interference Coordination. In ICC (pp. 3323-3328).
[41] Maghsudi, S., & Hossain, E. (2017). Distributed user association in energy harvesting dense small cell networks: A mean-field multi-armed bandit approach. IEEE Access, 5, 3513-3523.
[42] Henri, S., Vlachou, C., & Thiran, P. (2018) Multi-armed Bandit in Action: Optimizing Performance in Dynamic Hybrid Networks.
[43] Combes, R., & Proutiere, A. (2015). Dynamic rate and channel selection in cognitive radio systems. IEEE Journal on Selected Areas in Communications, 33(5), 910-921.
[44] Cano, C., & Neu, G. (2018). Wireless Optimisation via Convex Bandits: Unlicensed LTE/WiFi Coexistence. arXiv preprint arXiv:1802.04327.
[45] Anandkumar, A., Michael, N., Tang, A. K., & Swami, A. (2011). Distributed algorithms for learning and cognitive medium access with logarithmic regret. IEEE Journal on Selected Areas in Communications, 29(4), 731-745.
[46] Gai, Y., Krishnamachari, B., & Jain, R. (2010, April). Learning multiuser channel allocations in cognitive radio networks: A combinatorial multi-armed bandit formulation. In New Frontiers in Dynamic Spectrum, 2010 IEEE Symposium on (pp. 1-9). IEEE.
[47] Gai, Y., Krishnamachari, B., & Jain, R. (2012). Combinatorial network optimization with unknown variables: Multi-armed bandits with linear rewards and individual observations. IEEE/ACM Transactions on Networking (TON), 20(5), 1466-1478.
[48] Liu, K., & Zhao, Q. (2010). Distributed learning in multi-armed bandit with multiple players. IEEE Transactions on Signal Processing, 58(11), 5667-5681.
[49] Wilhelmi, F., Cano, C., Neu, G., Bellalta, B., Jonsson, A., & Barrachina-Muñoz, S. (2017). Collaborative Spatial Reuse in Wireless Networks via Selfish Multi-Armed Bandits. arXiv preprint arXiv:1710.11403.
[50] Wilhelmi, F., Barrachina-Muñoz, S., Cano, C., Bellalta, B., Jonsson, A., & Neu, G. (2018). Potential and Pitfalls of Multi-Armed Bandits for Decentralized Spatial Reuse in WLANs. arXiv preprint arXiv:1805.11083.